.

По аналогии с выражением

можно записать

.

При этом , величина называется поперечным волновым числом. Она определяет критическую длину волны.

При теоретическом анализе типов волн в прямоугольном волноводе необходимо решить однородные волновые уравнения

(для - волн)

(для - волн)

во внутренней области волновода (рисунок 1)

Решение должно удовлетворять граничным условиям на поверхности идеального проводника:

1). На поверхности стенок тангенциальная компонента вектора равна нулю.

2). На поверхности стенок нормальная компонента вектора равна нулю.

От координаты все компоненты поля зависят по закону .

Для волн типа получаем следующие выражения для компонент поля

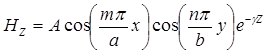
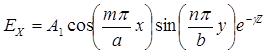
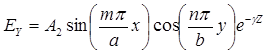(1)

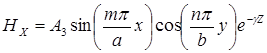
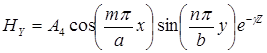
Для определения и получаем соотношения

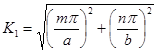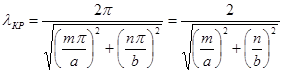; (2)

Здесь везде и , в коэффициенты , , , , входят все величины, не зависящие от координат.

Аналогичные по структуре выражения могут быть получены и для компонент поля волн типа .

Таким образом в прямоугольном волноводе может существовать бесконечное число волн типа и , отличающиеся друг от друга индексами и (а, значит, и выражениями для компонент поля и критической длины волны).

Какие минимальные значения могут принимать индексы и ?

Одновременно и и не могут быть равными нулю (при этом поле в волноводе отсутствует). Для волн типа один из индексов ( или ) может быть равен нулю, а другой – не равен нулю. Для волн типа ни один из индексов ( или ) не может быть равен нулю. Минимальное значение может быть .