откуда

Из условия равенства потерь можно записать:

(3.33)

Воспользовавшись полученными соотношениями можно получить:

(3.34)

Таким образом, зная активные потерн в стали и магнитный поток в сечении, можно определить Хщ.г, учитывающее в схеме замещения потери на вихревые токи и гистерезис.

Кроме реактивного магнитного сопротивления, сталь обладает также активным магнитным сопротивлением R

Аналогично электрической цепи можно ввести понятие удельного активного магнитного сопротивления

где рд — удельное активное магнитное сопротивление стали;

(3.35)

где Р0— потери на единицу массы сердечника; у — плотность; l и S — длина и сечение сердечника; рл-— удельное реактивное магнитное сопротивление стали;

(3.36)

где pz — полное удельное магнитное сопротивление стали.

Зависимость рл, p^Y и pz от индукции для стали Э-12 представлена на рис. Так как

(3.37)

Если задан поток Ф,„ и известны размеры участка •S и /, то сначала находят индукцию Bm = (&m/S, а затем по кривым, аналогичным рис.3.3, определяют рл, р*, Pz. Воспользовавшись (3.35), (3.36)и (3.37) можно вычислить магнитные сопротивления У? , X и %

Однако чаще дается кривая намагничивания на переменном токе, связывающая максимальное значение индукции Вт с действующим значением напряженности Н с учетом активных потерь.

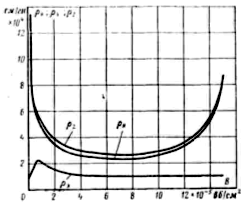
Рис.3.3 Удельные сопротивления стали.

(3.38)

Расчет магнитной цепи переменного тока ведется с помощью двух уравнений Кирхгофа в комплексной форме методом последовательных приближений.

Если задано напряжение на обмотке, ее активное сопротивление и размеры магнитной цепи, то сначала находят поток без учета сопротивления стали и активного сопротивления катушки из, а затем строят схемы замещения, уточняя каждый раз значения магнитных сопротивлений, потоков и н. с. Расчет производится до тех пор, пока потоки в рабочем зазоре двух соседних приближений будут отличаться друг от друга не более чем на 10%.