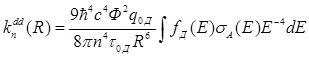, (1.4)

здесь – ориентационный фактор; и – квантовый выход и время жизни возбужденного состояния донора в отсутствии тушителя; – показатель преломления среды на частоте переноса энергии; и – нормированные спектр излучения донора и сечение поглощения акцептора соответственно.

Таким образом, согласно теории Ферстера, в случае диполь-дипольных взаимодействий вероятность переноса энергии пропорциональна силам осцилляторов переходов в доноре и акцепторе, интегралу перекрытия нормированного спектра излучения донора со спектром поглощения акцептора и обратно пропорциональна шестой степени расстояния между молекулами.

Позже теория Фёрстера была обобщена Декстером на случай мультипольных и обменных взаимодействий [11]. Дальнейшее ее развитие состояло в учете макроскопических параметров, влияющих в основном на константу скорости передачи энергии. При этом считается, что взаимодействие между компонентами донорно – акцепторной пары не влияет на константы скоростей как излучательной, так и безызлучательной дезактивации возбуждений акцептора, поскольку для приготовления начального и конечного квантовых состояний берутся невозмущенные волновые функции изолированных молекул донора и акцептора энергии в соответствующих состояниях. Именно это положение теории Фёрстера – Декстера подвергается критике в Новой теории переноса энергии, разрабатываемой в последнее время В.Я. Артюховым и Г.В. Майером. Перенос энергии за счет обменных взаимодействия становится актуальным, когда кулоновская часть электронного матричного элемента взаимодействия в (1.2) значительно меньше обменной

. (1.5)

Неравенство (1.5) выполняется для интеркомбинационных синглет-триплетных переходов в органических молекулах. Поэтому основной вклад в в этом случае дает обменный интеграл. Взаимодействия такого типа названы В.Л. Ермолаевым и А.Н. Терениным обменно-резонансными, и хотя в литературе известны и другие термины, этот термин наиболее широко используется в настоящее время специалистами.

Рассмотрим более подробно межмолекулярный триплет-триплетный перенос энергии электронного возбуждения, происходящий по обменно-резонансному механизму.

Если представить электронные волновые функции донора и акцептора в виде произведения координатной волновой функции на спиновую , то обменный интеграл имеет вид

. (1.6)

Здесь учтено, что описывает кулоновское взаимодействие, которое не действует на спиновые переменные.

Из (1.6) следует, что обменный интеграл , если

Возбужденное и основное состояния могут иметь разную мультипольность, т. е.

(1.7)

Следовательно, мультипольность состояний донора и акцептора после акта передачи должна измениться одновременно.

Учитывая, что спектр излучения донора и поглощения акцептора определяются интегралами Франка-Кондона и используя (1.3) Декстер [11] записал выражение для вероятности переноса энергии по обменно-резонансному механизму в следующем виде

(1.8)

здесь — нормированный спектр поглощения акцептора.

Поскольку величина обменных взаимодействий пропорциональна плотности перекрывания электронных облаков донора и акцептора энергии, которая экспоненциально убывает с расстоянием между ними, то параметр , в котором скрыта зависимость от расстояния, можно представить в виде , где L — средний эффективный боровский радиус.