где - намагниченность насыщения вещества частиц, - объемная концентрация дисперсной фазы в образце объемом .

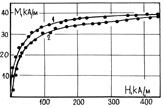
Рисунок 5. Кривые намагничения магнитных жидкостей, с одинаковой объемной концентрацией, но отличающихся средним размером дисперсных частиц (1-d=14нм, 2-d=9нм)

Таким образом, начальные участки кривых намагничивания магнитных жидкостей, имеющих одинаковую объемную концентрацию дисперсных частиц, должны иметь различную крутизну, определяемую характерным размером дисперсных частиц. На рисунке 5 приведены кривые намагничивания магнитных жидкостей с одинаковой объемной концентрацией магнетита, но различным диаметром частиц (d = 9 нм, d = 14 нм), полученные с помощью вибрационного магнетометра [15 Моя дисс.]. Как и следует из теории Ланжевена, для МЖ с большим магнитным моментом неравенство начинает выполняться при меньшем значении напряженности поля. Проведение расчетов с целью получения информации о процессе намагничивания из экспериментально полученных кривых требует знания функции распределения частиц по размером, выбор которой связан с некоторым произволом. Использование получивших в последнее время распространение компьютерных технологий позволяет непосредственное использование гистограмм распределения без аппроксимации их к конкретной функции. В этом случае, законом Ланжевена удобно пользоваться в виде:

, (1.10)

откуда для слабых полей

.

Последнее выражение легко представить [16?] в виде:

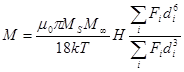, (1.11)

где - намагниченность насыщения вещества частицы (магнетита), - намагниченность насыщения магнитной жидкости (), - доля частиц с диаметром . С учетом того, что , для магнитной восприимчивости магнитной жидкости справедливо выражение:

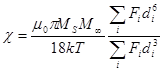(1.12)

Как видно из (1.10) зависимость крутизны начального участка кривой намагниченности от размера частиц определяется выражением , которая может быть найдена из гистограммы распределения дисперсных частиц по размерам. Сравнение (1.12) с (1.4) показывает, что при проведении магнитогранулометрических расчетов в области слабых полей с применением (1.4) в случае полидисперсности системы величина определяется выражением:

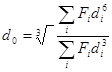(1.13)