Полагая, что пузырек сохраняет сферическую форму, запишем выталкивающую его архимедову силу , которая обусловлена различием плотностей жидкости и газа в пузырьке . Она определяется известной формулой:

.

В записанной формуле учтено, что .

Обсудим, как под действием архимедовой силы всплывает пузырек, который, двигаясь медленно, сохраняет сферическую форму.

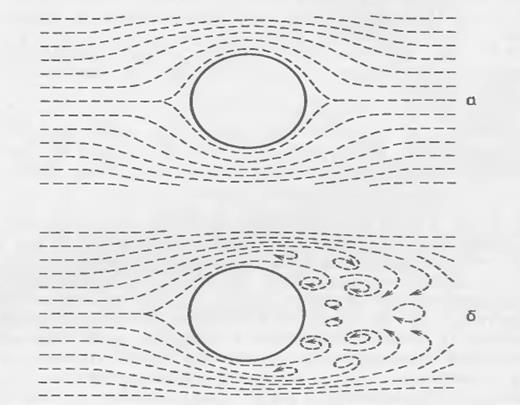
Рисунок 1 Схемы ламинарного (а) и турбулентного обтекания жидкостью движущегося в ней пузыря

Вокруг пузырька возникают потоки, которые перемещают жидкость от лобовой поверхности пузырька к его тыльной поверхности. Чем дальше от пузырька, тем с меньшей скоростью протекает жидкость, тем менее она «осведомлена», что в ней движется пузырек. В действительности, течет жидкость, а мы видим результат этого течения - всплывание пузырька. Поэтому скорость его всплывания должна зависеть и от того, как движется жидкость, и от его физических свойств.

«Медленным» будем называть такое движение пузырька, при котором перетекание воды от его лобовой к тыльной поверхности не сопровождается появлением завихрений, вода течет спокойно, как бы послойно и слои не перемешиваются между собой. Физики говорят «ламинарно». Путь, по которому движутся слои жидкости можно изобразить линиями (см рис 1. а). При ламинарном течении они не изламываются, взаимно не пересекаются и не пересекают сами себя. В потоке не появляются вихри. Соприкасающиеся слои жидкости получают информацию друг о друге вследствие их взаимного трения. При таком обтекании пузырька жидкостью установившаяся скорость его ламинарного всплывания должна зависеть от вязкости жидкости , от радиуса пузырька R и от силы F, действующей на пузырек.

Выясним связь между величинами , , R и F.

Естественно предположить, что скорость пропорциональна выталкивающей силе F, и тем меньше, чем больше радиус пузырька R и вязкость воды : .

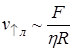Так как здесь обсуждается случай очень медленного всплывания пузырька в вязкой жидкости, то естественно предполагать, что энергия, передаваемая всплывающим пузырьком обтекающей его жидкости, главным образом расходуется на преодоление вязкого трения, а не придание жидкости кинетической энергии, которая должна зависеть от массы жидкости, а значит, и от ее плотности.

Перепишем нашу формулу в виде , учтем что , , , , и потребуем, чтобы размерность левой и правой частей нашей формулы совпадали. Мы убедимся, что , , , т.е. то, что и записано в нашей формуле.