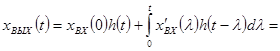
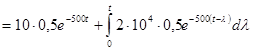.

Берем интеграл, приводим подобные члены, строим графики. Но в рамках курса ТОЭ РГРТУ требуется ответ до состояния

t≥10-3

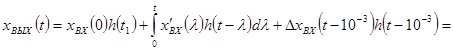
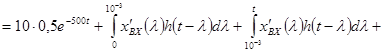
Применение импульсных характеристик

Известно, что

1) g(t)= -1{H(p)},

2) xвых(p)=xвх(p)H(p),

3) =,

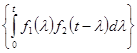Пусть , ,

тогда =-1=

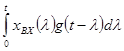
Фактически это есть другая форма интеграла Дюамеля, которая может быть получена используя связь g(t) и h(t). Порядок применения получения выражения такой же, но при численном нахождении интеграла удобней использовать собственно интеграл Дюамеля.

Применение передаточной функции

Если известно H(p) и xвх(t), можно записать изображение xвх(p), вычислить xвых(p)=H(p)xвх(p) и перейти к оригиналу.

Особенно удобно применять H(p)тогда, когда xвх(t) имеет простой вид, позволяющий легко записать изображение xвх(p) либо сразу для всего сигнала, либо разложение его на более простые компоненты и воспользовавшись принципом положения.

Например:

xвх(t)=10e-100t

, ,

, , ,

, ,

,

,

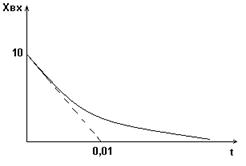
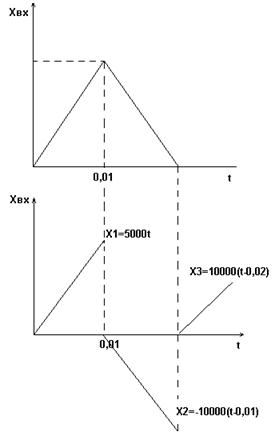
Этот входной сигнал можно представить в виде совокупности двух более простых. Тогда

1) Для 0 ≤t<10-2

,

2) Для t≥10-2, t<2∙10-2

3) .

Теперь умножая на H(p) находим изображающие реакции и затем переходим к оригиналу.